Questão 01 sobre Função Logarítmica para Ensino Médio: (UFMG) Observe a figura.
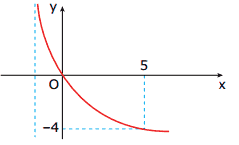
Nessa figura, está representado o gráfico da função f(x) = log2 . Então, f(1) é igual:
a) -3
b) -2
c) -1
d)
e)
Questão 02. (UFU-MG) No sistema de coordenadas cartesianas, considere os gráficos das funções y = ex e y = loge x, como mostra a figura a seguir. Considerando r // Ox e s // Oy, construímos o triângulo ABC. Assim, pode-se afirmar que a área desse triângulo, em unidades de área, é:
a) (e2-1)
b) (e-1)2
c) e2
d) (e-1)2
Questão 03. (EFOA-MG–2006) Seja f: (0, ∞) → R dada por f(x) = log4 x. Sabendo-se que a e b satisfazem as equações f(a) = 1 + f(b) e a – b = 3f(2), é CORRETO afirmar que a + b vale:
a)
b) 2
c) 3
d)
e)
Questão 04. (VUNESP) O par ordenado de números reais que não corresponde a um ponto do gráfico de y = log x é:
a) (9, 2.log 3)
b) (1, 0)
c)
d)
e) (–(52), –2.log5)
Questão 05 sobre Função Logarítmica para Ensino Médio: Modelo Enem. Uma das grandezas relacionadas ao som é a sua altura A, medida em decibéis (dB). A altura de um som está relacionada com a sua intensidade I, medida em watts por metro quadrado, através da função:
A(I) = 10.log, sendo I0 uma constante que vale 10-12
Sabe-se que as intensidades sonoras aproximadas de um carro e de um avião a jato são iguais a 10-4 e 102
, respectivamente.
Portanto, pode-se afirmar que a razão entre as alturas dos sons produzidos pelo avião e pelo carro, nessa ordem, é igual a:
A) 1,75
B) 1,85
C) 1,95
D) 2,05
E) 2,35
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas do simulado com exercícios de matemática sobre Função Logarítmica para Ensino Médio:
01. B;
02. D;
03. A;
04. E;
05. A
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
