Questão 01 sobre Trigonometria: Modelo Enem. Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual a fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2∝ . A figura ilustra essa situação:
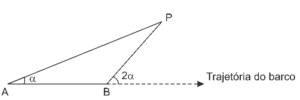
Suponha que o navegante tenha medido o ângulo α 30º e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB 2000m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será:
a) 1000 m .
b) 1000 √3 m .
c) 2000 ![]() m.
m.
d) 2000 m .
e) 2000 3 m .
Questão 02. Modelo Enem.
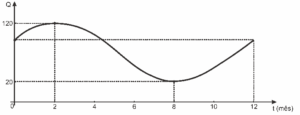
O gráfico mostra a quantidade de animais que uma certa área de pastagem pode sustentar ao longo de 12 meses. Propõe-se a função Q (t) = a sen (b + ct) + d para descrever essa situação. De acordo com os dados, Q (0) é igual a:
a) 100.
b) 97.
c) 95.
d) 92.
e) 90.
Questão 03. Modelo Enem. A figura a seguir apresenta o delta do rio Jacuí, situado na região metropolitana de Porto Alegre. Nele se encontra o parque estadual Delta do Jacuí, importante parque de preservação ambiental. Sua proximidade com a região metropolitana torna-o suscetível aos impactos ambientais causados pela atividade humana.
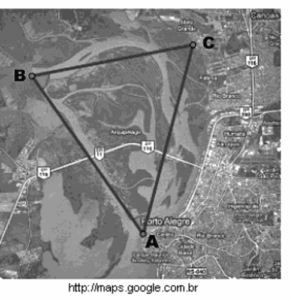
A distância do ponto B ao ponto C é de 8 km, o ângulo A mede 45° e o ângulo C mede 75°. Uma maneira de estimar quanto do Delta do Jacuí está sob influência do meio urbano é dada pela distância do ponto A ao ponto C. Essa distância, em km, é

Questão 04 sobre Trigonometria: Modelo Enem. Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, Franca, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.
Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.
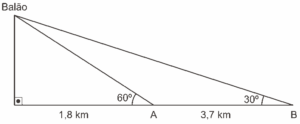
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°. Qual a altura aproximada em que se encontrava o balão?
a) 1,8 km
b) 1,9 km
c) 3,1 km
d) 3,7 km
e) 5,5 km
Questão 05. Modelo Enem. Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por:
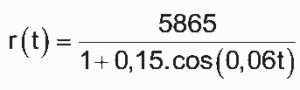
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S. O cientista deveria concluir que, periodicamente, S atinge o valor de:
a) 12 765 km.
b) 12 000 km.
c) 11 730 km.
d) 10 965 km.
e) 5 865 km.
Questão 06. Modelo Enem. Uma empresa precisa comprar uma tampa para o seu reservatório, que tem a forma de um tronco de cone circular reto, conforme mostrado na figura.
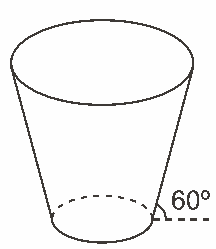
Considere que a base do reservatório tenha raio r = 2 √3 m e que sua lateral faça um ângulo de 60° com o solo. Se a altura do reservatório é 12 m, a tampa a ser comprada deverá cobrir uma área de

Questão 07 sobre Trigonometria: Modelo Enem. Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
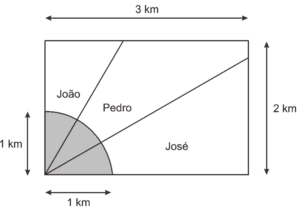
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a (considere ![]() = 0,58)
= 0,58)
a) 50%.
b) 43%.
c) 37%.
d) 33%.
e) 19%.
Questão 08 sobre Trigonometria: Modelo Enem. Considere um ponto P em uma circunferência de raio r no plano cartesiano. Seja Q a projeção ortogonal de P sobre o eixo x, como mostra a figura, e suponha que o ponto P percorra, no sentido anti-horário, uma distância d ≤ r sobre a circunferência.
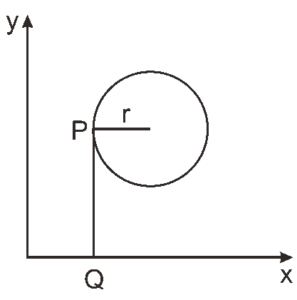
Então, o ponto Q percorrerá, no eixo x, uma distância dada por

Questão 09. Modelo Enem. Em determinada cidade, a concentração diária, em gramas, de partículas de fósforo na atmosfera é medida pela função  em que t é a quantidade de horas para fazer essa medição.
em que t é a quantidade de horas para fazer essa medição.
O tempo mínimo necessário para fazer uma medição que registrou 4 gramas de fósforo é de
a) 1/2 hora.
b) 1 hora.
c) 2 horas.
d) 3 horas.
e) 4 horas.
Questão 10 sobre Trigonometria: Modelo Enem. No último pleito, o horário de encerramento das votações, segundo determinação do TSE para todo o estado do Rio Grande do Sul, foi às 17 horas. Passados 5 minutos do encerramento, o menor ângulo entre os ponteiros do relógio era de
a) 123°
b) 122° 30′
c) 122°
d) 120° 30′
e) 120°
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das questões de matemática sobre Trigonometria:
1. B
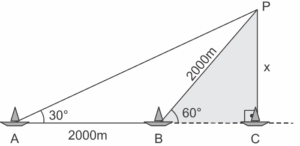
ΔABP é isósceles (AB = BP = 2000). No ΔPBC temos:
2. C
De acordo com o gráfico, temos a = 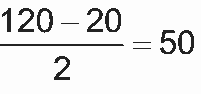
D = 120 – 50 = 70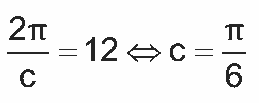
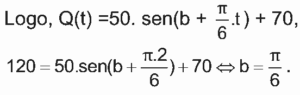 (continua após …70,…) substituindo o ponto ( 2,120) na função, temos:
(continua após …70,…) substituindo o ponto ( 2,120) na função, temos:
3. B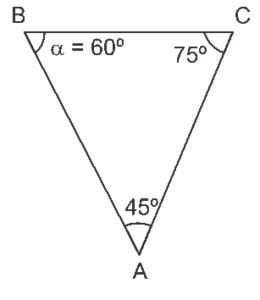
Aplicando o teorema dos senos, temos:
4. C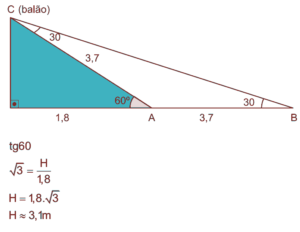
5. B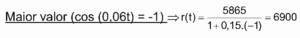
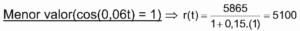
Somando, temos:
6900 + 5100 = 12000
6. B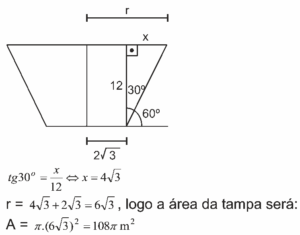
7. E
No triângulo assinalado (João) temos:
8. B
α = d/r (rad)
K = r.cos(d/R)
X = R – k
X = R – R.cos(d/r)
X= R(1-cos(d/R))
9. B
10.B
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
