Posições Relativas entre Ponto, Reta e Circunferência 10 Questões

Por

Questão 01 sobre Posições Relativas entre Ponto, Reta e Circunferência: (FGV)

a) No plano cartesiano, considere a circunferência de equação x2 + y2 – 4x = 0 e o ponto P(3, 3). Verificar se P é interior, exterior ou pertencente à circunferência.

b) Dada a circunferência de equação x2 + y2 = 9 e o ponto P(3, 5), obtenha as equações das retas tangentes à circunferência, passando por P.

Questão 02. (UEM) A equação da reta tangente à circunferência (x – 3)2 + (y – 2)2 = 25 no ponto (6, 6) é:

a) 3y – 4x + 6 = 0
b) 4y + 3x – 42 = 0
c) 4y + 3x – 6 = 0
d) 4y – 3y – 6 = 0
e) 3y + 4x – 42 = 0

Questão 03. (Esam-RN) A equação da circunferência com centro no ponto (28, 3), tangente externamente à circunferência (x – 4)2 + (y – 2)2 = 64, é:

a) (x – 8)2 + (y – 3)2 = 5
b) (x + 8)2 + (y – 3)2 = 25
c) (x + 8)2 + (y + 3)2 = 25
d) (x – 8)2 + (y + 3)2 = 25
e) (x + 8)2 + (y + 3)2 = 5

Questão 04 sobre Posições Relativas entre Ponto, Reta e Circunferência: (U.F. Pelotas)

Determinar a equação geral da circunferência concêntrica à circunferência x2 + y2 + 6x – 8y = 0 e tangente ao eixo das ordenadas.

Questão 05. (UPF 2015) Sabendo que o ponto P(4, 1) é o ponto médio de uma corda AB da circunferência x2 – 6x + y2 + 4 = 0, então a equação da reta que passa por A e B é dada por:

a) y = – x + 5
b) y = x + 5
c) y = – x + 3
d) y = x – 3
e) y = –1/2x + 5

Questão 06. (UEG 2015) Observe a figura a seguir.

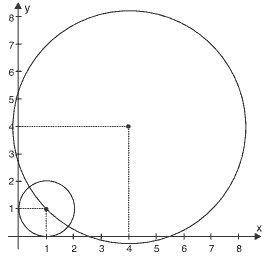
circunferência de maior raio e menor raio

Sabendo-se que a circunferência de maior raio passa pelo centro da circunferência de menor raio, a equação da circunferência de maior raio é:

a) x2 + y2 + 4x + 4y + 18 = 0
b) x2 + y2 – 4x – 4y – 14 = 0
c) x2 + y2 – 8x – 8y + 14 = 0
d) x2 + y2 + 8x + 8y + 18 = 0

Questão 07 sobre Posições Relativas entre Ponto, Reta e Circunferência: (UFOP-MG) Determine a equação da circunferência tangente ao eixo Ox, cujo centro é a intersecção das retas r: y = x + 5 e t: y = – 2x + 8.

Questão 08. (UPE 2016) Uma reta r de equação ax + by + c = 0 tangencia a circunferência β de equação x2 + y2 – 2x – 6y – 8 = 0 no ponto P = (– 2, 0). Qual é o valor de a + b + c?

a) 2
b) 3
c) 4
d) 5
e) 6

Questão 09. (UFJF 2016) Considere a circunferência C: (x – 1)2 + (y + 3)2 = 9.

a) Determine se o ponto A = (4, – 3) é interior, exterior ou pertencente à circunferência C.
b) Encontre o(s) valor(es) de para que a circunferência C e a reta y = ax possuam dois pontos em comum.

Questão 10 sobre Posições Relativas entre Ponto, Reta e Circunferência: (UECE 2015) No referencial cartesiano ortogonal usual, a medida da área do quadrilátero convexo cujos vértices são as interseções de cada uma das retas x + y – 1 = 0 e x + y + 1 = 0 com a circunferência x2 + y2 = 25, calculada com base na unidade de comprimento (u.c.) adotada no referencial cartesiano considerado, é:

a) 16 (u.c.)2.
b) 14 (u.c.)2.
c) 18 (u.c.)2.
d) 20 (u.c.)2.

Confira também estas listas de Exercícios:

  1. Posições Relativas 10 Questões Resolvidas
  2. O melhor simulado sobre Esferas Matemática
  3. 13 Questões e Exemplos de Progressão geométrica
  4. Lista de Exercícios com Equações e Problemas de Matemática
  5. Lista de Questões sobre Semelhança de Triângulos

🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.

Gabarito com as respostas do simulado com 10 questões de matemática sobre Posições Relativas entre Ponto, Reta e Circunferência:

01) a) Pertence
b) x – 3 = 0 ou 8x – 15y + 51 = 0;

02) b;
03) b;

04) (x + 3)2 + (y – 4)2 = 9;

05) a;
06) c;

07) (x – 1)2 + (y – 6)2 = 36;

08) c;

09) a) Pertence a C.
b) a < 0 ou a > 3/4;

10) b;

Deixe um comentário