Questão 01 sobre Inequações no Plano: (PUC) O semiplano hachurado é o conjunto dos pontos (x, y) tais que:
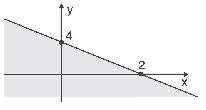
a) y < 2x + 4
b) y ≤ 2x + 4
c) y ≤ 4 – 2x
d) y < 4 – 2x
e) 2y ≤ x – 4
Questão 02. (UFRGS) Na figura abaixo:
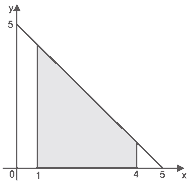
a região sombreada do plano xy é descrita pelas desigualdades da alternativa:
a) 0 ≤ x ≤ 4 e 0 ≤ y ≤ 5 – x
b) 0 ≤ x ≤ 5 e 0 ≤ y ≤ 5 + x
c) 1 ≤ x ≤ 4 e 0 ≤ y ≤ 5 – x
d) 1 ≤ x ≤ 4 e 0 ≤ y ≤ 5
e) 1 ≤ x ≤ 4 e 0 ≤ y ≤ 5 + x
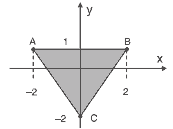
Questão 03. (Fuvest) Seja S a região do plano cartesiano representada pelo triângulo ABC e seu interior. Determine um sistema de inequações que caracterize os pontos (x, y) pertencentes a S.
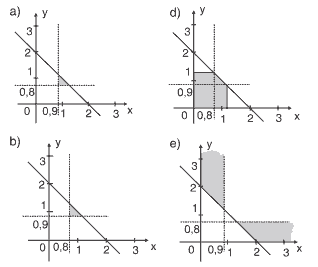
Questão 04 sobre Inequações no Plano: (UFTM) Uma pessoa em cadeira de rodas necessita de espaço mínimo para rotação de sua cadeira em um corredor que dá acesso a uma porta.
De acordo com as normas técnicas da da obra, a largura mínima (x) do corredor deve ser de 90 cm, a da porta (y) de 80 cm e, além disso, é necessário que a soma dessas duas medidas seja igual ou maior que 2 m.
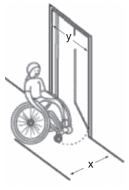
Uma representação no plano cartesiano ortogonal apenas dos pares (x, y), com ambas coordenadas dadas em metros, que atendem às normas técnicas da obra, é:
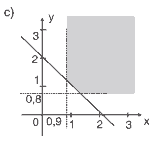
Questão 05. (FGV) A reta x + 3y – 3 = 0 divide o plano determinado pelo sistema cartesiano de eixos em dois semiplanos opostos. Cada um dos pontos (– 2, 2) e (5, b) está situado em um desses dois semiplanos. Um possível valor de b é:
a) 1/4
b) – 1/4
c) 3/4
d) – 3/4
e) – 1/2
Questão 06. (UFF) A Segunda Guerra Mundial motivou o estudo de vários problemas logísticos relacionados com o transporte e a distribuição de recursos. Muitos destes problemas podem ser modelados como um programa linear. Como um exemplo de programa linear, considere o problema de encontrar o par ordenado (x, y) que satisfaz simultaneamente as condições –2x + y ≥ 0, x ≥ 0, x – y + 2 ≥ 0, e cuja a soma das coordenadas x + y é máxima. Se (x0, y0) é a solução deste programa linear, é correto afirmar que:
a) x0 + y0 = 7
b) x0 + y0 = 6
c) x0 + y0 = 8
d) x0 + y0 = 2
e) x0 + y0 = 0
Questão 07. (UFRJ) Sejam a um número real positivo e S a região do plano cartesiano dada por S = {x, y} ∈ R2 | x ≤ a; y ≤ –a; y ≤ x} Considere, como de costume, que o quadrado U = {x, y} ∈ R2 | 0 ≤ x ≤ 1; 0 ≤ y ≤ 1} tem área de medida 1. Determine o valor de a para que a medida da área da região S seja igual a 18.
Questão 08 sobre Inequações no Plano: (FGV) No plano cartesiano:
a) represente graficamente os pontos (x, y) que satisfazem a relação: x + 2y ≤ 6;
b) ache a área do polígono determinado pelas relações simultâneas:
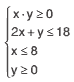
🔵 >>> Confira nossa lista completa de exercícios sobre Matemática.
Gabarito com as respostas das 08 atividades de matemática sobre Inequações no Plano:
1) c;
2) c;
3)
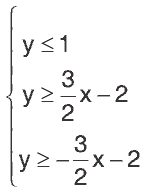
4) c;
5) d;
6) b;
7) a = 3;
8)
a) 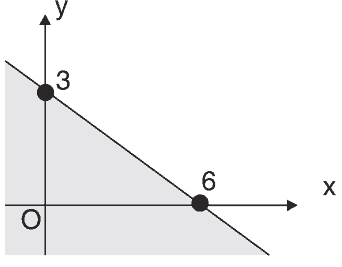
b) Área = 80
Doutorando em Genética e Biologia Molecular – UESC-BA
Mestre em Genética e Biologia Molecular – UESC-BA
Pós-Graduado em Metodologia do Ensino de Biologia e Química – FAEL
Licenciado em Ciências Biologias – IFMT/Campus Juína
